Transfert en cours..., vous êtes sur le "nouveau" serveur data.abuledu.org dont l'hébergement est financé par l'association abuledu-fr.org grâce à vos dons et adhésions !
Vous pouvez continuer à soutenir l'association des utilisateurs d'AbulÉdu (abuledu-fr.org) ou l'association ABUL.
Suivez la progression de nos travaux et participez à la communauté via la liste de diffusion.
Votre recherche ...
Nuage de mots clés
Photographie, Bouteilles, Mathématiciens, Noeuds et épissures, Travail du verre, Mathématiques récréatives, Ferdinand Möbius (1790-1868), Felix Klein (1849-1925)
Bouteille de Klein en verre
Réalisation de l'immersion de la bouteille de Klein, en verre. On peut en quelque sorte considérer que la bouteille de Klein est une surface qui fait un « nœud ». En tant que surface (objet à 2 dimensions), il lui faut 4 dimensions pour faire un nœud, de même que pour une courbe (objet à une dimension) il faut 3 dimensions pour faire un nœud.
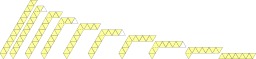
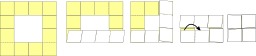
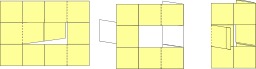
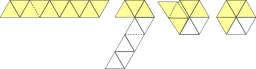
Construction et manipulation d'un hexahexaflexagone
Construction et manipulation d'un hexahexaflexagone en huit étapes.
Dessins et plans, Jeux mathématiques, Cercles, Géométrie des cercles, Mathématiques récréatives, Théodore Motzkin (1908-1970)
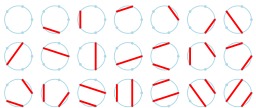
Cordes de Motzkin entre cinq points sur un cercle
Vingt-une cordes de Motzkin (qui ne se coupent pas) entre cinq points sur un cercle.
Dessins et plans, Jeux mathématiques, Cercles, Géométrie des cercles, Mathématiques récréatives, Théodore Motzkin (1908-1970)
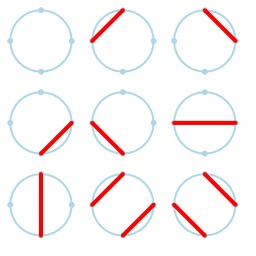
Cordes de Motzkin entre quatre points sur un cercle
Cordes de Motzkin sur un cercle : les neuf manières de dessiner des cordes qui ne se coupent pas entre quatre points d'un cercle. Le nombre de Motzkin est le nombre de façons de choisir des cordes ne se coupant pas, parmi les cordes reliant n points disposés sur un cercle. Source : http://fr.wikipedia.org/wiki/Nombre_de_Motzkin.
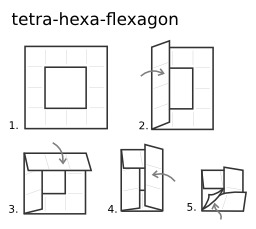
Flexagone
Hexahexaflexagone. Le flexagone est un objet topologique issu du ruban de Moebius, construit le plus souvent à l’aide d’une bande de papier pliée. Les préfixes que l’on peut ajouter au nom indiquent le nombre de faces différentes du flexagone puis son nombre de côtés. L'hexahexaflexagone a la forme d'un hexagone et possède six faces différentes. C’est une forme complexe du flexagone, fabriquée à partir d’une bande de papier de 18 triangles équilatéraux. Celle-ci est repliée sur elle-même de façon à avoir la longueur de 9 triangles, puis est ensuite pliée comme un trihexaflexgone. Source : http://fr.wikipedia.org/wiki/Flexagone
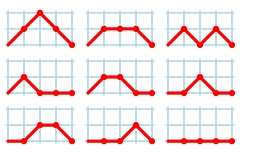
Interprétation du nombre de Motzkin pour quatre pas
Neuf chemins de Motzkin de (0, 0) à (4, 0), pour 4 pas en ne faisant que des pas Nord-Est, Est et Sud-Est. Les chemins sont en bijection avec les arbres. Source : http://fr.wikipedia.org/wiki/Nombre_de_Motzkin.
Dessins et plans, Géométrie, Jeux mathématiques, Rubans, Ruban adhésif, Mathématiques récréatives, Ferdinand Möbius (1790-1868), Collages (art)
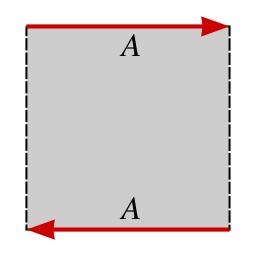
Montage d'un ruban de Möbius
Schéma de montage d'un ruban de Möbius : recoller les deux flèches en respectant le sens.
Photographie, Géométrie, Jeux mathématiques, Rubans, Ruban adhésif, Pliages en papier, Mathématiques récréatives, Ferdinand Möbius (1790-1868)
Ruban de Moebius
Ruban de Moebius construit à partir d'une bande de papier, un ruban adhésif retenant les deux bouts. Il est facile de visualiser la bande de Möbius dans l'espace : un modèle simple se réalise en faisant subir une torsion d'un demi-tour à une longue bande de papier, puis en collant les deux extrémités. En topologie, le ruban de Möbius (aussi appelé bande de Möbius ou boucle de Möbius) est une surface compacte dont le bord est homéomorphe à un cercle. Autrement dit, il ne possède qu'une seule face contrairement à un ruban classique qui en possède deux. Elle a la particularité d'être réglée et non-orientable. Source : http://fr.wikipedia.org/wiki/Ruban_de_M%C3%B6bius.
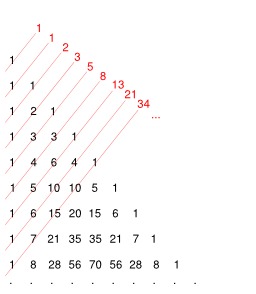
Dessins et plans, Arithmétique, Treizième siècle, Blaise Pascal (1623-1662), Mathématiques, Lapins, Triangle de Pascal, Populations d'animaux, Suite de Fibonacci
La suite de Fibonacci
Triangle de Pascal et suite de Fibonacci : La somme des diagonales ascendantes du triangle de Pascal forme la suite de Fibonacci. Leonardo Fibonacci (v. 1175-1250). Elle doit son nom à Leonardo Fibonacci, dit Leonardo Pisano, un mathématicien italien du XIIIe siècle qui, dans un problème récréatif posé dans un de ses ouvrages, le Liber Abaci, décrit la croissance d'une population de lapins : « Un homme met un couple de lapins dans un lieu isolé de tous les côtés par un mur. Combien de couples obtient-on en un an si chaque couple engendre tous les mois un nouveau couple à compter du troisième mois de son existence ? » Cette suite est fortement liée au nombre d'or, φ (phi). Ce nombre intervient dans l'expression du terme général de la suite. Inversement, la suite de Fibonacci intervient dans l'écriture des réduites de l'expression de φ (phi) en fraction continue : les quotients de deux termes consécutifs de la suite de Fibonacci sont les meilleures approximations du nombre d'or.
Photographie, Géométrie, Boîtes à jeux, Engrenages en plastique, Jeux et récréations, Loisirs créatifs, Spirographes
Spirographe
Instrument de loisir créatif. Le Spirographe, marque déposée par Hasbro, est un instrument de dessin permettant de tracer des figures géométriques, des courbes mathématiques techniquement connues sous le nom d'hypotrochoïdes. Le Spirographe a été inventé par Denys Fisher, qui l'a présenté en 1965 au Salon du jouet de Nuremberg. Les droits de distribution ont été acquis par Kenner, qui l'introduit sur le marché américain en 1966. Le Spirographe est composé de différentes roues et d'anneaux dentés en plastique transparent. Les roues sont les pièces mobiles, et se positionnent dans les anneaux, pièces fixes, de manière à pouvoir y tourner grâce au système d'engrenages.